22  Sequential hypothesis testing

Author

Affiliation

Aditya Mahajan

McGill University

Consider a decision maker (DM) that makes a series of i.i.d. observations which may be distributed according to PDF \(f_0\) or \(f_1\). Let \(Y_t\) denote the observaion at time \(t\). The DM wants to differentiate between two hypothesis: \[\begin{gather*} h_0 : Y_t \sim f_0 \\ h_1 : Y_t \sim f_1 \end{gather*}\] Typically, we think of \(h_0\) as the normal situation (or the null hypothesis) and \(h_1\) as an anomaly. For example, the hypothesis may be \[ h_0: Y_t \sim {\cal N}(0, σ^2) \quad h_1: Y_t \sim {\cal N}(μ, σ^2) \] or \[ h_0: Y_t \sim \text{Ber}(p) \quad h_1: Y_t \sim \text{Ber}(q). \]

Let the random variable \(H\) denote the value of the hypothesis. The a priori probability \(\PR(H = h_0) = p\).

The system continues for a finite time \(T\). At each \(t < T\), the DM has three options:

• stop and declare \(h_0\)
• stop and declare \(h_1\)
• continue and take another measurement

At the terminal time step \(T\), the continuation option is not available. Each measurement has a cost \(c\). When the DM takes a stopping action \(ν\), it incurs a stopping cost \(\ell(ν, H)\).

We typically assume \(\ell(h_0, h_0) = \ell(h_1, h_1) = 0\). The term \(\ell(h_1, h_0)\) indicates that the DM declares an anomaly when everything is okay. This is called false alarm penalty. The term \(\ell(h_0, h_1)\) indicates that DM declares everything is okay when there is an anomaly. This is called the missed detection penalty.

Let \(τ\) denote the time when the DM stops. Then the total cost of running the system is \(cτ + \ell(ν, H)\). The objective is to find the optimal stopping strategy that minimize the expected total cost.

22.1 Dynamic programming decomposition

We use the belief-state as an information state to obtain a dynamic programming decomposition. Recall that the beief state is two-dimensional pdf where \[ b_t(h) = \PR(H = h | Y_{1:t}), \quad h \in \{h_0, h_1\}. \]

Remarks

• We are only conditioning on \(Y_{1:t}\) and not adding \(A_{1:t-1}\) in the conditioning. This is because we are taking the standard approach used in optimal stopping problems where we are only defining the state for case when the stopping decision hasn’t been taken so far and all previous actions are continue. Taking a continue action does not effect the observations. For this reason, we do not condition on \(A_{1:t-1}\).

• It is possible to exploit the fact that \(b_t = [p_t, 1 - p_t]^T\) and write a simplified DP in terms of \(p_t\). In these notes, I don’t make this simplification so that we can see how these results will extend to the case of non-binary hypothesis.

The dynamic program for the above model is then given by \[ V_T(b_T) = \min\{ \EXP[ \ell(h_0, H) | B_T = b_T], \EXP[ \ell(h_1, H) | B_T = b_T] \} \] and for \(t \in \{T-1, \dots, 1\}\), \[ V_t(b_t) = \min \{ \EXP[ \ell(h_0, H) | B_t = b_t], \EXP[ \ell(h_1, H) | B_t = b_t], c + \EXP[V_{t+1}(ψ(b_t, Y_{t+1})) | B_t = b_t] \}, \] where \(ψ(b, y)\) denotes the standard non-linear filtering update (there is no dependence on \(a\) here because there are no state dynamics in this model).

We introduce some notation to simplify the discussion. Define

• \(L_i(b) = \EXP[ \ell(h_i, H) | B = b] = \sum_{h \in \{h_0, h_1\}} \ell(h_i, h) b(h)\).
• \(W_t(b_t) = c + \EXP[V_{t+1}(ψ(b_t, Y_{t+1})) | B_t = b_t]\).

Then, the above DP can be written as \[ V_T(b_T) = \min\{ L_0(b_T), L_1(b_T) \} \] and for \(t \in \{T-1, \dots, 1\}\), \[ V_t(b_t) = \min \{ L_0(b_t), L_1(b_t), W_t(b_t) \}. \]

22.2 Structure of the optimal policy

We start by establishing simple properties of the different functions defined above.

Lemma 22.1 The above functions statisfy the following properties:

• \(L_i(b)\) is linear in \(b\).
• \(V_t(b)\) and \(W_t(b)\) is concave in \(b\).
• \(V_t(b)\) and \(W_t(b)\) are increasing in \(t\).

An illustration of the minimum of two straight lines and a concave function. Move the points around to see how the shape of the function changes.

Proof

The linearity of \(L_i(b)\) follows from definition. From the discussion on POMDPs, we know that \(V_{t+1}(b)\) is concave in \(b\) and so is \(\EXP[V_{t+1}(ψ(b, Y_{t+1})) | B_t = b]\). Therefore \(W_t(b)\) is concave in \(b\).

Finally, by construction, we have that \(V_{T-1}(b) \le V_T(b)\). The monotonicity in time then follows from Q2 of Assignment 2. Sincen \(V_t\) is monotone in time, it implies that \(W_t\) is also monotone.

Now define stopping sets \(D_t(h) = \{ b \in Δ^2 : π_t(b) = h \}\) for \(h \in \{h_0, h_1\}\). The key result is the following.

Theorem 22.1 For all \(t\) and \(h \in \{h_0, h_1\}\), the set \(D_t(h)\) is convex. Moreover, \(D_t(h_i) \subseteq D_{t+1}(h_i)\).

An illustration of the stopping sets. Move the points around to see how the shape of the stopping set changes.

Proof

Note that we can write \(D_t(h) = A_t(h) \cap B_t(h)\), where \[ A_t(h_i) = \{ b \in Δ^2 : L_i(b) \le L_j(b) \} \quad\text{and}\quad B_t(h_i) = \{ b \in Δ^2 : L_i(b) \le W_t(b) \}. \]

\(A_t(h_i)\) is a the set of \(b\) where one linear function of \(b\) is less than or equal to another linear function of \(b\). Therefore, \(A_t(h_i)\) is a convex set.

Similarly, \(B_t(h_i)\) is the set of \(b\) where a linear function of \(b\) is less than or equal to a concave function of \(b\). Therefore \(B_t(h_i)\) is also a convex set.

\(D_t(h_i)\) is the intersection of two convex sets, and hence convex.

The monotonicty of \(D_t(h_i)\) in time follows from the monotonicity of \(W_t\) in time.

Theorem 22.2 Suppose the stopping cost satisfy the following: \[\begin{equation} \label{eq:cost-ass} \ell(h_0, h_0) \le c \le \ell(h_0, h_1) \quad\text{and}\quad \ell(h_1, h_1) \le c \le \ell(h_1, h_0). \end{equation}\] Then, \(e_i \in D_t(h_i)\), where \(e_i\) denotes the standard unit vector (i.e., \(e_0 = [1, 0]^T\) and \(e_1 = [0, 1]^T\)).

Remark

The assumption on observation cost states that: (i) the cost of observation is greater than the cost incurred when the DM chooses the right hypothesis, and (ii) the cost of observation is less than the cost incurred when the DM chooses the wrong hypothesis. Both these assumptions are fairly natural.

Proof

Note that \(L_i(e_0) = \ell(h_i, h_0)\) and \(L_i(e_1) = \ell(h_1, h_1)\). Moreover, by construction, \(W_t(b) \ge c\). Thus, under the above assumption on the cost, \[ L_0(e_0) = \ell(h_0, h_0) \le c \le W_t(e_0) \] and \[ L_0(e_0) = \ell(h_0, h_0) \le \ell(h_1, h_0) = L_1(e_0). \] Thus, \(e_0 \in D_t(h_0)\).

By a symmetric argument, we can show that \(e_1 \in D_t(h_1)\).

Theorem 22.1 and Theorem 22.2 imply that the optimal stopping regions are convex and include the “corner points” of the simplex. Note that although we formulated the problem for binary hypothesis, all the steps of the proof hold in general as well.

Stopping regions for multiple hypothesis

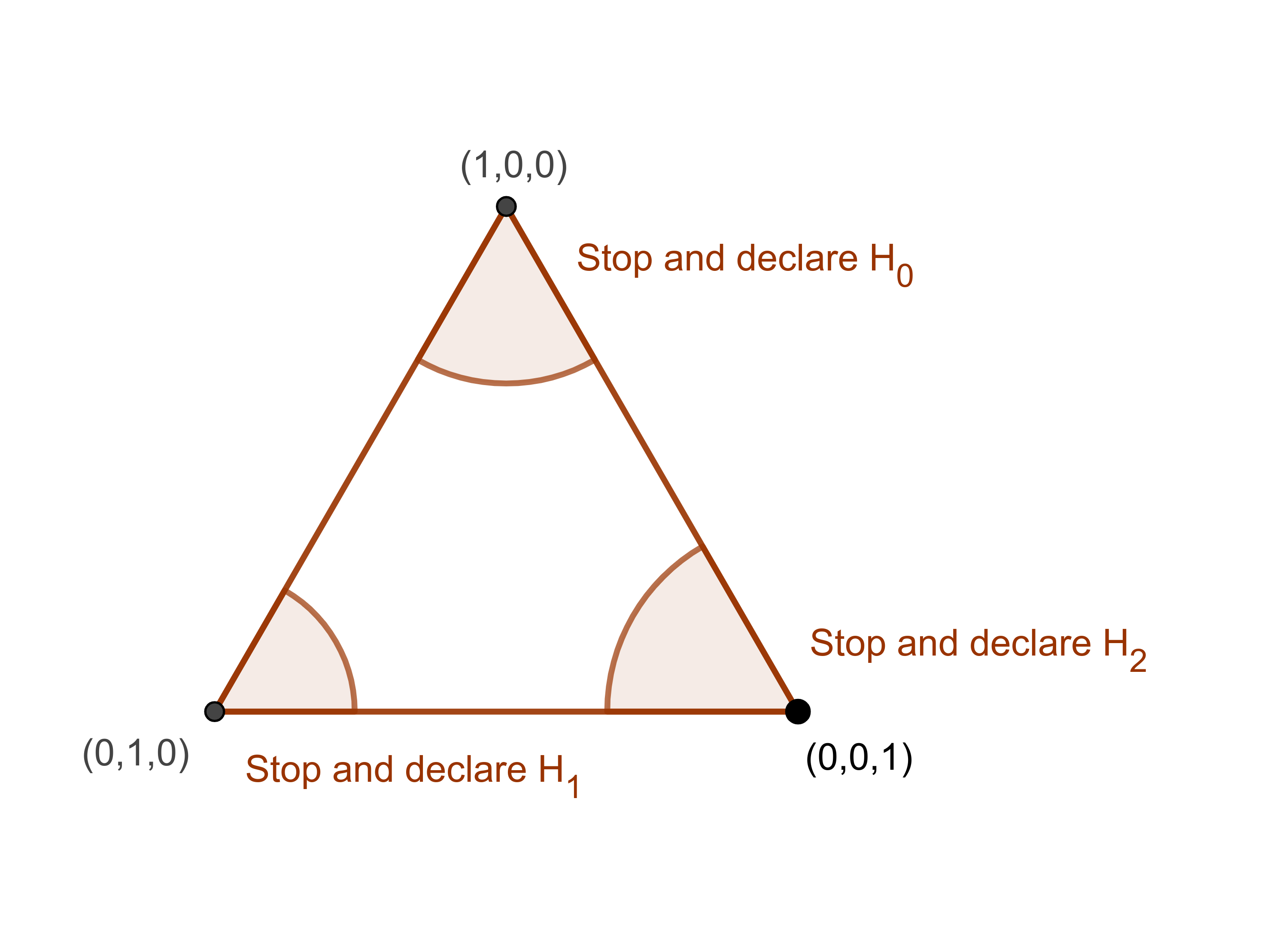
For binary hypothesis, we can present a more concerete characterizatin of the optimal policy. Note that the two-dimensional simplex is equivalent to the interval \([0,1]\). In particular, any \(b = Δ^2\) is equal to \([p, 1-p]\), where \(p \in [0,1]\). Now define:

• \(\displaystyle β_t = \min\left\{ p \in [0, 1] : π_t\left(\begin{bmatrix} p \\ 1-p \end{bmatrix}\right) = h_0 \right\}.\)
• \(\displaystyle α_t = \max\left\{ p \in [0, 1] : π_t\left(\begin{bmatrix} p \\ 1-p \end{bmatrix}\right) = h_1 \right\}.\)

Then, by definition, the optimal policy has the following threshold property:

Proposition 22.1 Let \(\bar π_t(p) = π_t([p, 1-p]^T)\). Then, under \eqref{eq:cost-ass}, \[ \bar π_t(p) = \begin{cases} h_1, & \text{if } p \le α_t \\ \mathsf{C}, & \text{if } α_t < p < β_t \\ h_0, & \text{if } β_t \le p. \end{cases} \]

Furthermore, the decision thresholds are monotone in time. In particular, for all \(t\), \[ α_t \le α_{t+1} \le β_{t+1} \le β_t. \]

The above property is simplies stated slighted in terms of the likelihood ratio. In particular, define \(λ_t = b_t(0)/b_t(1) = p_t/(1 - p_t)\). Then, we have the following:

Proposition 22.2 Let \(\hat π_t(λ) = π_t([λ/(1+λ), 1/(1+λ)]^T)\). Then, under \eqref{eq:cost-ass}, \[ \hat π_t(λ) = \begin{cases} h_1, & \text{if } λ \le α_t/(1 - α_t) \\ \mathsf{C}, & \text{if } α_t/(1 - α_t) < λ < β_t/(1 - β_t)_t \\ h_0, & \text{if } β_t/(1 - β_t)_t \le λ. \end{cases} \]

Proof

For any \(β, β \in [0, 1]\), \[ α \le β \iff \frac{α}{1-α} \le \frac{β}{1-β}.\]

The result of Proposition 22.2 is called the sequential likelihood ratio test (SLRT) or sequential probability ratio test (SPRT) to contrast it with the standard :likelihood ratio test in hypotehsis testing.

22.3 Infinite horizon setup

Assume that \(T = ∞\) so that the continuation alternative is always available. Then, we have the following.

Theorem 22.3 Under \eqref{eq:cost-ass}, an optimal decision rule always exists, is time-homogeneous, and is given by the solution of the following DP: \[ V(b) = \min\{ L_0(b) , L_1(b) , W(b) \} \] where \[ W(b) = c + \int_{y} [ pf_0(y) + (1-p)f_1(y)] V(ψ(b,y)) dy. \]

Therefore, the optimal thresholds \(a\) and \(b\) are time-homogeneous.

Proof

The result follows from standard results on non-negative dynamic programming. We did not cover non-negative DP. Essentially it determines conditions under which undiscounted infinite horizon problems have a solution when the per-step cost is non-negative.

22.4 Upper bound on the expected number of measurements

For simplicity, we assume that \(\ell(h_0, h_0) = \ell(h_1, h_1) = 0\). For the infinite horizon model, we can get upper bound on the expected number of measurements that an optimal policy will take. Let \(τ\) denote the number of measurements taken under policy \(π\) and \(A_τ\) denote the terminal action after stopping. Then, the performance of policy \(π\) is given by \[ J(π) = \EXP[ c τ + \ell(H, A_\tau) \mid \Pi = b ]. \] Note that \(\ell(H, A_\tau) \ge 0\). Therefore, the performance of the optimal policy is lower bounded by \[ J^* \ge c\, \EXP^{π^*}[ τ \mid \Pi = b] . \] Now, consider a policy \(\tilde π\) which does not consider continuation action and takes the best stopping decision. The performance of \(\tilde π\) is given by \[ J(\tilde π) = \min \{ \ell(h_1, h_0) b_1, \ell(h_0, h_1) b_0 \}. \] Since \(J(\tilde π) \ge J^*\), we get \[ \EXP^{π^*}[ τ \mid \Pi = b ] \le \frac 1c \min \{ \ell(h_1, h_0) b_1, \ell(h_0, h_1) b_0 \}. \]

Exercises

Exercise 22.1 Consider the following modification of the sequential hypothesis testing. As in the model discussed above, there are two hypothesis \(h_0\) and \(h_1\). The a priori probability that the hypothesis is \(h_0\) is \(p\).

In contrast to the model discussed above, there are \(N\) sensors. If the underlying hypothesis is \(h_i\) and sensor \(m\) is used at time \(t\), then the observation \(Y_t\) is distrubted according to pdf (or pmf) \(f^m_i(y)\). The cost of using sensor \(m\) is \(c_m\).

Whenever the decision maker takes a measurement, he picks a sensor \(m\) uniformly at random from \(\{1, \dots, N\}\) and observes \(Y_t\) according to the distribution \(f^m_i(\cdot)\) and incurs a cost \(c_m\).

The system continues for a finite time \(T\). At each time \(t < T\), the decision maker has three options: stop and declare \(h_0\), stop and declare \(h_1\), or continue to take another measurement. At time \(T\), the continue alternative is unavailable.

1. Formulate the above problem as a POMDP. Identify an information state and write the dynamic programming decomposition for the problem.

2. Show that the optimal control law has a threshold property, similar to the threshold propertly for the model described above.

Exercise 22.2 In this exercise, we will derive an approximate method to compute the performance of a given threshold based policy for infinite horizon sequential hypothesis testing problem. Let \[ θ_i(π,p) = \EXP^{π}[ τ | H = h_i] \] denote the expected number of samples when using stopping rule \(π\) assuming that the true hypothesis is \(h_i\). Note that for any belief state based stopping rule, \(θ_i\) depends on the initial belief \([p, 1-p]\). Furthermore, let \[ ξ_i(h_k ;π, p) = \PR^π(A_τ = h_k | H = h_i) \] denote the probability that the stopping action is \(h_k\) when using stopping rule \(π\) assuming that the true hypothesis is \(h_i\).

1. Argue that the performance of any policy \(π\) can be written as \[\begin{align*} V_π(p) &= c [ p θ_0(π, p) + (1-p) θ_1(π,p) ] \\ & \quad + p \sum_{a \in \{h_0, h_1\}} \ell(a, h_0) ξ_0(a; π, p) \\ & \quad + (1-p) \sum_{a \in \{h_0, h_1\}} \ell(a, h_1) ξ_1(a; π, p). \end{align*}\] Thus, approximately computing \(θ_i\) and \(ξ_i\) gives an approximate value of \(V_π(p)\).

2. Now assume that the policy \(π\) is of a threshold form with thresholds \(a\) and \(b\). To avoid trivial cases, we assume that \(p \in (a,b)\). The key idea to compute \(θ_i\) and \(ξ_i\) is that the evolution of \(p_t = \PR(H = h_t | Y_{1:t})\) is a Markov chain which starts at a state \(p \in (a,b)\) and stops the first time \(p_t\) goes below \(a\) or above \(b\).

   

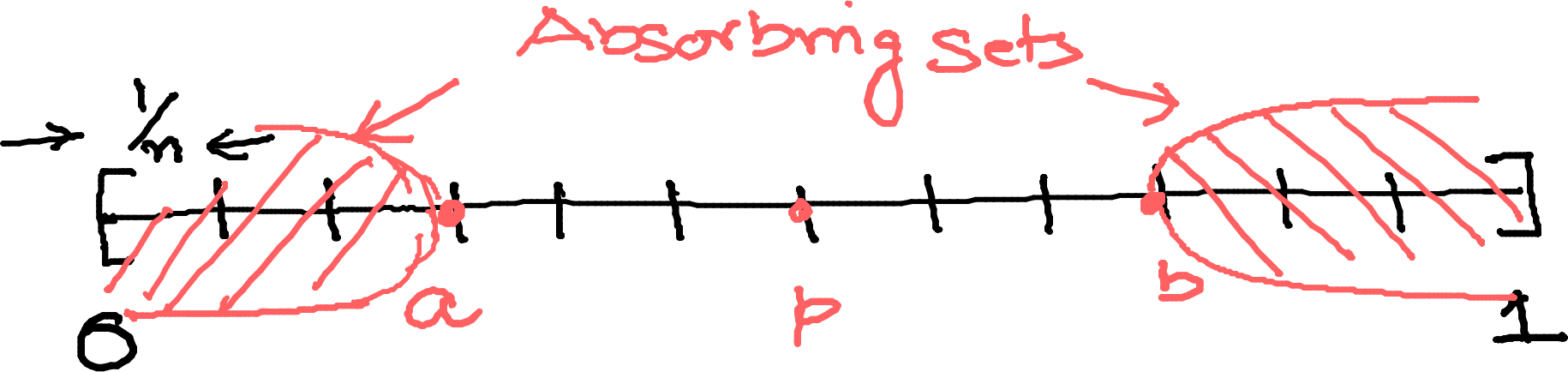
   Discretization of the state space

   Suppose we discretize the state space space \([0, 1]\) into \(n+1\) grid points \(\ALPHABET D_n = \{0, \frac1n, \dots, 1\}\). Assume that \(p\), \(a\), and \(b\) lie on this discrete grid. Discreteize \(p_t\) to the closest grid point and let \(P_i\) denote the transition matrix of the discretized \(p_t\) when the true hypothesis is \(h_i\). Partition the \(P_i\) as \[ \left[\begin{array}{c|c|c} A_i & B_i & C_i \\ \hline D_i & E_i & F_i \\ \hline G_i & H_i & J_i \end{array}\right] \] where the lines correspond to the index for \(a\) and \(b\). The transition matrix of the absorbing Markov chain is given by \[ \hat P_i = \left[\begin{array}{c|c|c} I & 0 & I \\ \hline D_i & E_i & F_i \\ \hline I & 0 & I \end{array}\right] \] Now suppose \(j\) is the index of \(p\) in \(\ALPHABET D_n\). Using properties of absorbing Markov chains, show that

   • \(ξ_i(h_0; \langle a, b \rangle, p) \approx [ (I - E_i)^{-1} F_i \mathbf{1} ]_j\)
   • \(ξ_i(h_1; \langle a, b \rangle, p) \approx [ (I - E_i)^{-1} D_i \mathbf{1} ]_j\)
   • \(θ_i(\langle a, b \rangle, p) \approx [ (I - E_i)^{-1} \mathbf{1} ]_j\)

Notes

For more details on sequential hypothesis testing, incuding an approximate method to determine the thresholds, see Wald (1945). The optimal of sequential likelihood ratio test was proved in Wald and Wolfowitz (1948). The model described above was first considered by Arrow et al. (1949). See DeGroot (1970).

The upper bound on expected number of measurements is adapted from an argument presented in Hay et al. (2012).

Exercise 22.1 is from Bai et al. (2015). Exercise 22.2 is from Woodall and Reynolds (1983).

---

Arrow, K.J., Blackwell, D., and Girshick, M.A. 1949. Bayes and minimax solutions of sequential decision problems. Econometrica 17, 3/4, 213. DOI: 10.2307/1905525.

Bai, C.-Z., Katewa, V., Gupta, V., and Huang, Y.-F. 2015. A stochastic sensor selection scheme for sequential hypothesis testing with multiple sensors. IEEE transactions on signal processing 63, 14, 3687–3699.

DeGroot, M. 1970. Optimal statistical decisions. Wiley-Interscience, Hoboken, N.J.

Hay, N., Russell, S., Tolpin, D., and Shimony, S.E. 2012. Selecting computations: Theory and applications. UAI. Available at: http://www.auai.org/uai2012/papers/123.pdf.

Wald, A. 1945. Sequential tests of statistical hypotheses. The Annals of Mathematical Statistics 16, 2, 117–186. DOI: 10.1214/aoms/1177731118.

Wald, A. and Wolfowitz, J. 1948. Optimum character of the sequential probability ratio test. The Annals of Mathematical Statistics 19, 3, 326–339. DOI: 10.1214/aoms/1177730197.

Woodall, W.H. and Reynolds, M.R. 1983. A discrete markov chain representation of the sequential probability ratio test. Communications in Statistics. Part C: Sequential Analysis 2, 1, 27–44. DOI: 10.1080/07474948308836025.