19  Lipschitz MDPs

Author

Affiliation

Aditya Mahajan

McGill University

Keywords

MDPs, discounted MDPs - inventory management, lipschitz continuity

19.1 Preliminaries

Lipschitz continuous functions

Given two metric spaces \((\ALPHABET X, d_X)\) and \((\ALPHABET Y, d_Y)\), the Lipschitz constant of function \(f \colon \ALPHABET X \to \ALPHABET Y\) is defined by \[ \| f\|_{L} = \sup_{x_1 \neq x_2} \left\{ \frac{ d_Y(f(x_1), f(x_2)) } { d_X(x_1, x_2) } : x_1, x_2 \in \ALPHABET X \right\} \in [0, ∞]. \] The function is called Lipschitz continuous if its Lipschitz constant is finite.

Intuitively, a Lipschitz continuous function is limited by how fast it can change. For example, the following image from Wikipedia shows that for a Lipschitz continuous function, there exists a double cone (white) whose origin can be moved along the graph so that the whole graph always stays outside the double cone.

Image credit: https://en.wikipedia.org/wiki/File:Lipschitz_Visualisierung.gif

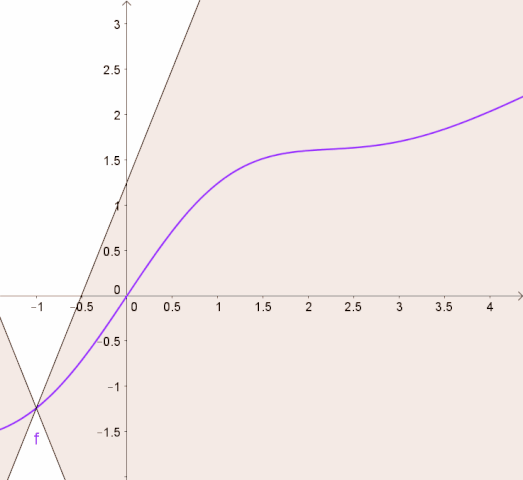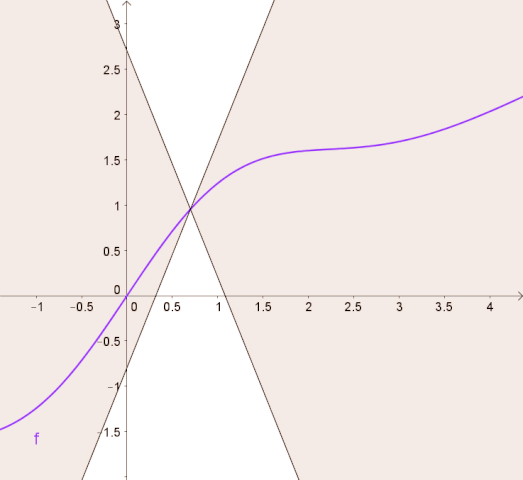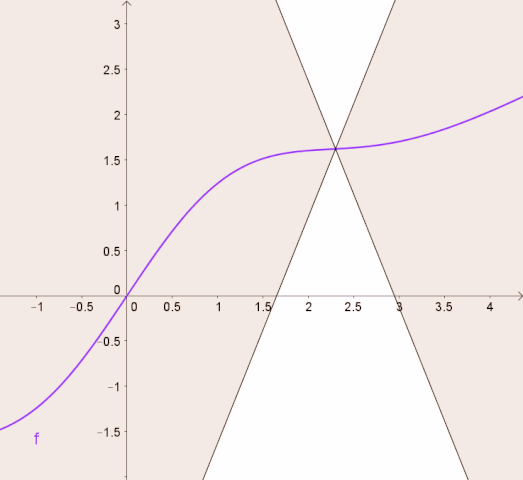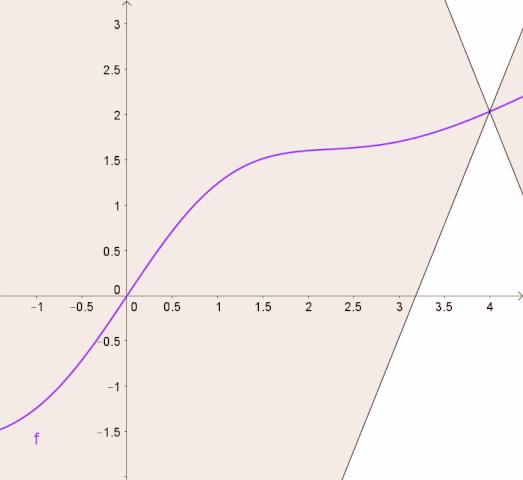
Let \(\ALPHABET Z\) be an arbitrary set. A function \(f \colon \ALPHABET X × \ALPHABET Z \to \ALPHABET Y\) is said to be uniformly Lipschitz in \(u\) if \[ \sup_{z \in \ALPHABET Z} \| f(\cdot, z) \|_L = \sup_{z \in \ALPHABET Z} \sup_{x_1 \neq x_2} \dfrac{ d_Y(f(x_1,z), f(x_2, z)) }{ d_X(x_1, x_2) } < ∞. \]

Some examples

A function \(f \colon \reals \to \reals\) is Lipschitz continuous if and only if it has bounded first derivative. The Lipschitz constant of such a function is equal to the maximum absolute value of the derivative.

Here are some examples of Lipschitz continuous functions:

1. The function \(f(x) = \sqrt{x^2 + 1}\) defined over \(\reals\) is Lipschitz continuous because it is everywhere differentiable and the maximum value of the derivative is \(L = 1\).

2. The function \(f(x) = |x|\) defined over \(\reals\) is Lipschitz continuous with Lipschitz constant equal to \(1\). Note that this function is continuous but not differentiable.

3. The function \(f(x) = x + \sin x\) defined over \(\reals\) is Lipschitz continuous with a Lipschitz constant equal to \(1\).

4. The function \(f(x) = \sqrt{x}\) defined over \([0,1]\) is not Lipschitz continuous because the function becomes infinitely steep as \(x\) approaches \(0\).

5. The function \(f(x) = x^2\) defined over \(\reals\) is not Lipschitz continuous because it becomes arbitrarily steep as \(x\) approaches infinity.

6. The function \(f(x) = \sin(1/x)\) is bounded but not Lipschitz because becomes infinitely steep as \(x\) approaches \(0\).

Properties of Lipschitz functions

Proposition 19.1 Lipschitz continuous functions have the following properties:

1. If a function \(f \colon (\ALPHABET X, d_X) \to (\ALPHABET Y, d_Y)\) is Lipschitz continuous, then \(f\) is uniformly continuous and measurable.

2. \(\| f\|_L = 0\) if and only if \(f\) is a constant.

3. If \(f \colon (\ALPHABET X, d_X) \to (\ALPHABET Y, d_Y)\) and \(g \colon (\ALPHABET Y, d_Y) \to (\ALPHABET Z, d_Z)\) are Lipschitz continuous, then \[ \| f \circ g \|_L \le \| f \|_L \cdot \| g \|_L. \]

4. The \(\| \cdot \|_{L}\) is a seminorm on the vector space of Lipschitz functions from a metric space \((\ALPHABET X, d_X)\) to \((\ALPHABET Y, d_Y)\). In particular, \(\| \cdot \|_L\) has the following properties: \(\| f \|_L \in [0, ∞]\), \(\| α f\|_L = |α| \cdot \|f\|_L\) for any \(α \in \reals\), and \(\| f_1 + f_2 \|_L \le \|f_1 \|_L + \|f_2 \|_L\).

5. Given a family of functions \(f_i\), \(i \in I\), on the same metric space such that \(\sup_{i \in I} f_i < ∞\), \[ \| \sup_{i \in I} f_i \|_{L} \le \sup_{i \in I} \| f_i \|_{L}. \]

6. Let \(f_n\), \(n \in \integers_{\ge 1}\), and \(f\) be functions from \((\ALPHABET X, d_X)\) to \((\ALPHABET Y, d_Y)\). If \(f_n\) converges pointwise to \(f\) for \(n \to ∞\), then \[ \| f \|_{L} \le \lim\inf_{n \to ∞} \| f_i \|_{L}. \]

19.2 Wasserstein distance

Let \(\mu\) and \(\nu\) be probability measures on \((\ALPHABET X, d_X)\). The Wasserstein distance between distributions \(\mu\) and \(\nu\) is defined as:¹ \[ K(\mu,\nu) = \sup_{f : \| f\|_L \le 1 } \left| \int_{\ALPHABET X} f\, d\mu - \int_{\ALPHABET X} f\, d\nu \right|. \]

¹ The definition provided here is actually the dual of the standard definition of Wasserstein distance. See Theorem 36.1 for details.

The next results follow immediately from the definition of Wasserstein distance.

Proposition 19.2 For any Lipschitz function \(f \colon (\ALPHABET X, d_X) \to (\reals, \lvert \cdot \rvert)\), and \(μ,ν\) are probability measures on \((\ALPHABET X, d_X)\), \[ \left| \int_{\ALPHABET X} f\, dμ - \int_{\ALPHABET X} f\, dν \right| \le \| f \|_L \cdot K(μ,ν). \]

The Wasserstein distance is a special class metrics on probability spaces known as integral probability meterics (IPMs). Proposition 19.2 is a special case of a similar general result for IPMs (Proposition 36.4).

Some examples

1. Let \((\ALPHABET X, d_X)\) be a metric space and for any \(x,y \in \ALPHABET X\), let \(δ_x\) and \(δ_y\) denote the Dirac delta distributions centered at \(x\) and \(y\). Then, \[ K(δ_x, δ_y) = d_X(x,y). \]

2. Let \((\ALPHABET X, d_X)\) be a Euclidean space with Euclidean norm. Let \(μ \sim \mathcal{N}(m_1, \Sigma_1)\) and \(ν \sim \mathcal{N}(m_2, \Sigma_2)\) be two Gaussian distributions on \(\ALPHABET X\). Then, \[K(μ,ν) = \sqrt{ \| m_1 - m_2 \|_2^2 + \text{Tr}( \Sigma_1 + \Sigma_2 - 2(\Sigma_2^{1/2} \Sigma_1 \Sigma_2^{1/2})^{1/2} ) }. \] If the two covariances commute, i.e. \(\Sigma_1\Sigma_2 = \Sigma_2 \Sigma_1\), then, \[K(μ,ν) = \sqrt{ \| m_1 - m_2 \|_2^2 + \| \Sigma_1^{1/2} - \Sigma_2^{1/2} \|^2_F},\] where \(\| ⋅ \|_{F}\) denotes the Frobeinus norm of a matrix.

   When \(\Sigma_1 = \Sigma_2\), we have \[K(μ,ν) = \| m_1 - m_2 \|_2. \]

3. If \(\ALPHABET X = \reals\) and \(d_X = | \cdot |\), then for any two distributions \(μ\) and \(ν\), \[\begin{equation}\label{eq:Kantorovich-CDF} K(μ,ν) = \int_{-∞}^∞ \left| F_μ(x) - F_ν(x) \right| dx, \end{equation}\] where \(F_μ\) and \(F_ν\) denote the CDF of \(μ\) and \(ν\).

   Furthermore, if \(μ\) is stochastically dominated by \(ν\), then \(F_μ(x) \ge F_ν(x)\). Thus, \[\begin{equation}\label{eq:Kantorovich-stochastic-dominance} K(μ, ν) = \bar μ - \bar ν \end{equation}\] where \(\bar μ\) and \(\bar ν\) are the means of \(μ\) and \(ν\).

19.3 Lipschitz MDPs

Consider an MDP where the state and action spaces are metric spaces. We use \(d_S\) and \(d_A\) to denote the corresponding metric. For ease of exposition, we define a metric \(d\) on \(\ALPHABET S × \ALPHABET A\) by \[ d( (s_1, a_1), (s_2, a_2) ) = d_S(s_1, s_2) + d_A(a_1, a_2). \]

We allow for randomized policies. Thus, given any state \(s \in \ALPHABET S\), \(π(\cdot | s)\) is a probability distribution on \(\ALPHABET A\). We say that a (possibly) randomized policy \(π\) has a Lipschitz constant of \(L_π\) if for any \(s_1, s_2 \in \ALPHABET S\), \[ K(π(\cdot| s_1), π(\cdot | s_2)) \le L_π d_S(s_1, s_2). \]

Note that if \(π\) is deterministic, then due to property of Kantorovich distance between delta distributions, the above relationship simplifies to \[ d_A(π(s_1), π(s_2)) \le L_π d_S(s_1, s_2). \]

Definition 19.1 An MDP is \((L_c, L_p)\)-Lipschitz if for all \(s_1, s_2 \in \ALPHABET S\) and \(a_1, a_2 \in \ALPHABET A\),

• \(| c(s_1, a_1) - c(s_2, a_2) | \le L_c\bigl( d_S(s_1, s_2) + d_A(a_1, a_2) \bigr)\).
• \(K(p(\cdot | s_1, a_1), p(\cdot | s_2, a_2)) \le L_p\bigl( d_S(s_1, s_2) + d_A(a_1, a_2) \bigr)\).

Example 19.1 As an example, consider the inventory management problem considered earlier. We assume that \(\ALPHABET S = \reals\) and \(\ALPHABET A = \reals_{\ge 0}\); the cost function and the dynamics are the same as before. We will show that this model is \((L_c, L_p)\) Lipschitz with \[ L_c = p + \max\{ c_h, c_s \} \quad\text{and}\quad L_p = 1. \]

Proof of Lipschitz continuity of the inventory model

Note that in this model, the per-step cost depends on the next stage, so we need to make the appropriate changes to compute \(L_c\).

We first consider \(L_p\). For random variables \(X \sim μ\) and \(Y \sim ν\), we will use the notation \(K(X,Y)\) to denote \(K(μ,ν)\). Let \(y_1 = s_1 +a_1\) and \(y_2 = s_2 + a_2\). Then, \[ K(p(\cdot | s_1, a_1), p( \cdot | s_2, a_2)) = K( y_1 - W, y_2 - W ) = K( W - y_1, W - y_2) \] where we have used the following fact that \(K(X,Y) = K(-X,-Y)\). Now observe that if \(y_1 > y_2\), the CDF of the RV \(W - y_1\) lies above the CDF of the RV \(W - y_2\); thus \(W - y_2\) [stochastically dominates] \(W - y_1\), hence from \(\eqref{eq:Kantorovich-stochastic-dominance}\), \(K(W - y_1, W - y_2) = y_1 - y_2\). By symmetry, if \(y_1 < y_2\), \(K(W - y_1, W - y_2) = y_2 - y_1\). Thus, \[ K( W - y_1, W - y_2) = | y_1 - y_2 | \le | s_1 - s_2 | + | a_1 - a_2| \] The above relationship implies \(L_p = 1\).

Now consider \[ \bar c(s,a) = \EXP[ c(s,a,S_{+}) \mid S = s, A = a] = pa + \EXP[ h(s+a - W) ] \] Then \[\begin{align*} | \bar c(s_1, a_1) - \bar c(s_2, a_2) | &\le p| a_1 - a_2 | + \| h \|_L K(s_1 + a_1 - W, s_2 + a_2 - W) \\ &\stackrel{(a)}\le p| a_1 - a_2 | + \| h \|_L | s_1 + a_1 - s_2 - a_2 | \\ &\le (p + \| h\|_L)[ |s_1 - s_2| + |a_1 - a_2| ] \end{align*}\] where \((a)\) follows from Proposition 19.2. Thus, \(L_c = p + \|h\|_L\).

Lipschitz continuity of Bellman updates

We now prove a series of results for the Lipschitz continuity of Bellman updates.

Lemma 19.1 Let \(V \colon \ALPHABET S \to \reals\) be \(L_V\)-Lipschitz continuity. Define \[ Q(s,a) = c(s,a) + γ \int V(y) p(y|s,a)dy. \] Then \(Q\) is \((L_c + γ L_p L_V)\)-Lipschitz continuous.

Proof

Consider, \[\begin{align*} | Q(s_1, a_1) - Q(s_2, a_2) | &\stackrel{(a)}\le | c(s_1, a_1) - c(s_2, a_2) | \\ & \quad + γ \left|\int V(y) p(y|s_1, a_1) dy - \int V(y) p(y|s_2, a_2) dy \right| \\ &\stackrel{(b)}\le L_c d( (s_1, a_1), (s_2, a_2) ) + γ L_V L_p d( (s_1, a_1), (s_2, a_2) ), \end{align*}\] where \((a)\) follows from the triangle inequality and \((b)\) follows from Proposition 19.2. Thus, \(L_Q = L_c + γ L_p L_V\).

Lemma 19.2 Let \(Q \colon \ALPHABET S × \ALPHABET A \to \reals\) be \(L_Q\)-Lipschitz continuous. Define \[V(s) = \min_{a \in \ALPHABET A} Q(s,a).\] Then \(V\) is \(L_Q\)-Lipschitz continuous.

Proof

Consider \(s_1, s_2 \in \ALPHABET S\) and let \(a_1\) and \(a_2\) denote the corresponding optimal action. Then, \[ \begin{align*} V(s_1) - V(s_2) &= Q(s_1, a_1) - Q(s_2, a_2) \\ &\stackrel{(a)}\le Q(s_1, a_2) - Q(s_2, a_2) \\ &\stackrel{(b)}\le L_Q( d_S(s_1, s_2) + d_A(a_2, a_2) )\\ &= L_Q d_S(s_1, s_2). \end{align*} \]

By symmetry, \[ V(s_2) - V(s_1) \le L_Q d_S(s_2, s_1). \] Thus, \[ | V(s_1) - V(s_2) | \le L_Q d_S(s_1, s_2). \] Thus, \(V\) is \(L_Q\)-Lipschitz continuous.

Lemma 19.3 Let \(Q \colon \ALPHABET S × \ALPHABET A \to \reals\) be \(L_Q\)-Lipschitz continuous and \(π\) be a (possibly randomized) \(L_π\)-Lipschitz policy. Define \[V_π(s) = \int Q(s, a) π(a | s) du.\] Then, \(V_π\) is \(L_Q( 1 + L_π)\)-Lipschitz continuous.

Proof

For any \(s_1, s_2 \in \ALPHABET S\), consider \[ \begin{align} | V_π(s_1) - V_π(s_2) | &= \left| \int Q(s_1, a) π(a | s_1) du - \int Q(s_2, a) π(a | s_2) du \right| \notag \\ &\stackrel{(a)}\le \left| \int Q(s_1, a) π(a | s_1) du - \int Q(s_2, a) π(a | s_1) du \right| \notag \\ & \quad + \left| \int Q(s_2, a) π(a | s_1) du - \int Q(s_2, a) π(a | s_2) du \right| \label{eq:split} \end{align} \] where \((a)\) follows from the triangle inequality. Now we consider both terms separately.

The first term of \eqref{eq:split} simplifies as follows: \[\begin{align} \left| \int Q(s_1, a) π(a | s_1) du - \int Q(s_2, a) π(a | s_1) du \right| &\stackrel{(b)}\le \int \left|Q(s_1, a) - Q(s_2, a)\right| π(a | s_1) du \notag \\ &\stackrel{(c)}\le \int L_Q d_S(s_1, s_2) π(a | s_1) du \notag \\ &= L_Q d_S(s_1, s_2), \label{eq:first} \end{align} \] where \((b)\) follows from the triangle inequality and \((c)\) follows from Lipschitz continuity of \(Q\).

The second term of \eqref{eq:split} simplifies as follows: \[ \begin{align} \left| \int Q(s, a) π(a | s_1) du - \int Q(s,a) π(a | s_2) du \right| &\stackrel{(d)}\le L_Q K (π(\cdot | s_1), π(\cdot | s_2)) \notag \\ &\stackrel{(e)}\le L_Q L_π d_S(s_1, s_2), \label{eq:second} \end{align} \] where the \((d)\) inequality follows from Proposition 19.2 and \((e)\) follows from the definition of Lipschitz continuous policy.

Substituting \eqref{eq:first} and \eqref{eq:second} in \eqref{eq:split}, we get \[ \begin{align*} | V_π(s_1) - V_π(s_2) | &\le L_Q d_S(s_1, s_2) + L_Q L_π d_S(s_1, s_2) \\ &= L_Q(1 + L_π) d_S(s_1, s_2). \end{align*} \] Thus, \(V\) is Lipschitz continuous with Lipschitz constant \(L_Q(1 + L_π)\).

19.4 Lipschitz continuity of value iteration

Lemma 19.4 Consider a discounted infinite horizon MDP which is \((L_c, L_p)\)-Lipschitz. Start with \(V^{(0)} = 0\) and recursively define

• \(\displaystyle Q^{(n+1)}(s,a) = c(s,a) + γ \int V^{(n)}(y) p(y|s,a) dy.\)
• \(\displaystyle V^{(n+1)}(s) = \min_{a \in \ALPHABET A} Q^{(n+1)}(s,a).\)

Then, \(V^{(n)}\) is Lipschitz continuous and its Lipschitz constant \(L_{V^{(n)}}\) satisfies the following recursion: \[L_{V^{(n+1)}} = L_c + γ L_p L_{V^{(n)}}.\]

Proof

We prove the result by induction. For \(n=1\), \(Q^{(1)}(s,a) = c(s,a)\), which is Lipschitz with Lipschitz constant \(L_{Q^{(1)}} = L_c\). Then, by Lemma 19.2, \(V^{(1)}\) is Lipschitz with Lipschitz constant \(L_{V^{(1)}} = L_{Q^{(1)}} = L_c\). This forms the basis of induction. Now assume that \(V^{(n)}\) is \(L_{V^{(n)}}\)-Lipschitz. Then, by Lemma 19.1, \(Q^{(n+1)}\) is \((L_c + γL_p L_{V^{(n)}})\)-Lipschitz. Therefore, by Lemma 19.2, \(V^{(n+1)}\) is Lipschitz with constant \[ L_{V^{(n+1)}} = L_c + γ L_p L_{V^{(n)}}.\]

Lemma 19.5 Consider a discounted infinite horizon MDP which is \((L_c, L_p)\)-Lipschitz and let \(π\) be any randomized time-homogeneous policy which is \(L_π\)-Lipschitz. Start with \(V^{(0)} = 0\) and then recursively define

• \(V^{(n)}_π(s) = \int Q^{(n)}_π(s,a)π(a|s) du.\)
• \(\displaystyle Q^{(n+1)}_π(s,a) = c(s,a) + γ \int V^{(n)}_π(y) p(y|s,a) dy.\)

Then, then \(Q^{(n)}_π\) is Lipschitz continuous and its Lipschitz constant \(L_{Q^{(n)}_π}\) satisfies the follwoing recursion: \[ L_{Q^{(n+1)}_π} + L_c + γ(1 + L_π)L_p L_{Q^{(n)}_π}. \]

Proof

We prove the result by induction. For \(n=1\), \(Q^{(1)}_π(s,a) = c(s,a)\), which is Lipschitz with Lipschitz constant \(L_{Q^{(1)}_π} = L_c\). This forms the basis of induction. Now assume that \(Q^{(n)}_π\) is \(L_{Q^{(n)}_π}\)-Lipschitz. Then, by Lemma 19.3, \(V^{(n)}_π\) is Lipschitz with Lipschitz constant \(L_{V^{(n)}_π} = L_{Q^{(n)}_π}(1 + L_π)\) and by Lemma 19.1, \(Q^{(n+1)}_π\) is Lipschitz with Lipschitz constant \(L_{Q^{(n+1)}_π} = L_c + γL_p L_{V^{(n)}_π}.\) Combining these two we get \[ L_{Q^{(n+1)}_π} + L_c + γ(1 + L_π)L_p L_{Q^{(n)}_π}. \]

Theorem 19.1 Given any \((L_c, L_p)\)-Lipschitz MDP, if \(γ L_p < 1\), then the infinite horizon \(γ\)-discounted value function \(V\) is Lipschitz continuous with Lipschitz constant \[ L_{V} = \frac{L_c}{1 - γ L_p} \] and the action-value function \(Q\) is Lipschitz with Lipschitz constant \[ L_Q = L_V = \frac{L_c}{1 - γ L_p}. \]

Proof

Consider the sequence of \(L_n = L_{V^{(n)}}\) values. For simplicity write \(α = γ L_p\). Then the sequence \(\{L_n\}_{n \ge 1}\) is given by: \(L_1 = L_c\) and for \(n \ge 1\), \[ L_{n+1} = L_c + α L_n. \] Hence, \[ L_n = L_c + α L_c + \dots + α^{n-1} L_c = \frac{1 - α^n}{1 - α} L_c. \] This sequence converges if \(|α| < 1\). Since \(α\) is non-negative, this is equivalent to \(α < 1\), which is true by hypothesis. Hence \(L_n\) is a convergent sequence. At convergence, the limit \(L_V\) must satisfy the fixed point of the recursion relationship introduced in Lemma 19.4, hence \[ L_V = L_c + γ L_p L_V. \] Consequently, the limit is equal to \[ L_V = \frac{L_c}{1 - γ L_p}. \] The Lipschitz constant of \(Q\) follows from Lemma 19.1.

Example 19.1 (continued)

As discussed in Example 19.1, the inventory management example is \((p + \max\{c_h,c_s\}, 1)\)-Lipschitz. Therefore, Theorem 19.1 implies that the value function of the inventory management problem is \(L_V\)-Lipschitz with \[ L_V = \frac{p + \max\{ c_h + c_s \}}{1 - γ}. \]

Later, in the notes on model approximation, we show that the bound on the Lipschitz constant is useful to understand the approximation error if we use a policy designed for a model with a slightly different demand distribution.

To understand the tightness of this bound, we consider a specific instance of inventory management problem where the demand is \(\text{Exp}(1)\), \(c_h = 2\), \(c_s = 5\), and \(p = 1\). The theoretical maximum value of the Lipschitz constant (for \(γ = 0.9\)) is \(L_V = 60\). In Figure 19.1, we show the animation of this upper bound, in the style of the wikipedia animation shown at the beginning of this lecture.

Figure 19.1: Animation showing the upper bound on the Lipschitz constant of the value function, computed via Theorem 19.1.

Note that since the demand is \(\text{Exp}(1)\), most of the mass of the demand is in the range \([0,10]\). So, the region of the value function of interest is perhaps \([-20,20]\) or so. We plot a larger region to highlight the fact that the bound on the Lipschitz constant has to capture the Lipschitz constant of the value function over the entire real line.

Theorem 19.2 Given any \((L_c, L_p)\)-Lipschitz MDP and an \(L_π\)-Lipschitz (possibly randomized) time-homogeneous policy \(π\), if \(γ (1 + L_π) L_p < 1\), then the infinite horizon \(γ\)-discounted value-action function \(Q_π\) is Lipschitz continuous with Lipschitz constant \[ L_{Q_π} = \frac{L_c}{1 - γ(1 + L_π) L_p} \] and the value function \(V_π\) is Lipschitz with Lipschitz constant \[ L_{V_π} = L_{Q_π}(1 + L_π) = \frac{L_c(1 + L_π)}{1 - γ(1 + L_π) L_p}. \]

Remark

The restrictive assumption in the result is that \(γ(1 + L_π)L_p < 1\). For a specific model, even when this assumption does not hold, it may be possible to directly check if the \(Q\)-function is Lipschitz continuous. Such a direct check often gives a better Lipschitz constant.

Proof

Consider the sequence of \(L_n = L_{Q^{(n)}_π}\) values. For simplicity, write \(α = γ(1 + L_π)L_p\). Then, the sequence \(\{L_n\}_{n \ge 1}\) is given by: \(L_1 = L_c\) and for \(n \ge 1\), \[L_{n+1} = L_c + α L_n. \] Hence, \[ L_n = L_c + α L_c + \dots + α^{n-1} L_c = \frac{1 - α^n}{1 - α} L_c. \] This sequence converges if \(|α| < 1\). Since \(α\) is non-negative, this is equivalent to \(α < 1\), which is true by hypothesis. Hence \(L_n\) is a convergent sequence. At convergence, the limit \(L_{Q_π}\) must satisfy the fixed point of the recursion relationship introduced in Lemma 19.5, hence \[ L_{Q_π} = L_c + γ(1 + L_π)L_p L_{Q_π}. \] Consequently, the limit is equal to \[ L_{Q_π} = \frac{L_c}{1 - γ(1 + L_π) L_p}. \]

The Lipschitz constant of \(V_π\) follows from Lemma 19.3.

19.5 Influence Radius

When the \(Q\)-function of an MDP is Lipschitz continuous, then the optimal action does not change too abruptly. More precisely, suppose an action \(a\) is optimal at state \(s\). Then, we can identify a hyperball \(B(s, ρ(s))\) of radius \(ρ(s)\) centered around \(s\) such that \(a\) is guaranteed to be the dominating action in \(ρ(s)\). This radius \(ρ(s)\) is called the influence radius.

Let \(π\) denote the optimal policy, i.e., \[ π(s) = \arg \min_{a \in \ALPHABET A} Q(s,a) \] and \(h\) denote the second best action, i.e., \[ h(s) = \arg \min_{a \in \ALPHABET A \setminus \{π(s)\}} Q(s,a). \] Define the domination value of state \(s\) to be \[ Δ(s) = Q(s, h(s)) - Q(s, π(s)). \]

Theorem 19.3 For a Lipschitz continuous \(Q\)-function, the influence radius at state \(s\) is given by \[ ρ(s) = \frac{ Δ(s) }{ 2 L_Q }. \]

Remark

Combining Theorem 19.2 and Theorem 19.3 implies that under the condition of Theorem 19.2, the influence radius at state \(s\) is at least \[ ρ(s) = Δ(s)(1 - γ(1 + L_π)L_p)/2L_c. \]

Proof

The intuition behind the proof is the following. The value of the action \(π(s)\) can only decrease by \(L_Q ρ(s)\) in \(B(s, ρ(s))\), while the value of the second best action \(h(s)\) can only increase by \(L_Q ρ(s)\). So, the shortest distance \(ρ(s)\) from \(s\) needed for an action \(h(s)\) to “catch-up” with action \(π(s)\) should satisfy \(2 L_Q ρ(s) = Δ(s)\) or \(ρ(s) = Δ(s)/2L_Q\).

Formally, for any \(s' \in B(s,ρ(s))\), \(d_S(s,s') \le ρ(s)\). Thus, for any action \(a \in \ALPHABET A\), \[ | Q(s,a) - Q(s',a)| \le L_Q d_S(s,s') \le L_Q ρ(s). \] Equivalently, \[ Q(s,a) - L_Q ρ(s) \le Q(s',a) \le Q(s,a) + L_Q ρ(s) \] which states that as \(s'\) moves away from \(s\), the value of \(Q(s',a)\) remains within a symmetric bound that depends on the radius \(ρ(s)\). Since this bound holds for all \(a\), they also hold for \(a = π(s)\). Thus, \[ Q(s, π(s)) - L_Q ρ(s) \le Q(s', π(s)) \le Q(s, π(s)) + L_Q ρ(s). \]

Since \(π(s)\) is the optimal action, for any other action \(a \neq π(s)\), \[ Q(s,π(s)) \le Q(s,a). \] Thus, the action \(π(s)\) is optimal as long as the upper bound on \(Q(s', π(s))\) is lower than the lower bound on \(Q(s',a)\), i.e., \[ Q(s, π(s)) + L_Q ρ(s) \le Q(s,a) - L_Q ρ(s). \] Thus, the maximum value of \(ρ(s)\) is when the relationship holds with equality, i.e., \[ ρ(s) = \frac{Q(s,a) - Q(s,π(s))}{2 L_Q} \ge \frac{Δ(s)}{2 L_Q}. \]

---

Exercises

Exercise 19.1 Let \((\ALPHABET S, d_S)\) be a metric space and \(s, s' \in \ALPHABET S\). Consider two Bernoulli measures \[ μ = a δ_s + (1-a) δ_{s'}, \qquad ν = b δ_s + (1-b) δ_{s'}. \]

Show that \[ K(μ,ν) = |a - b| d(s,s'). \]

Notes

The material in this section is taken from Rachelson and Lagoudakis (2010) and Hinderer (2005).

The proof of Lipschitz continuity for the inventory management problem in Example 19.1 is adapted from Müller (1997). Later, in the notes on model approximation, we show that the bound on the Lipschitz constant is useful to understand the approximation error if we use a policy designed for a model with a slightly different demand distribution.

Hinderer, K. 2005. Lipschitz continuity of value functions in Markovian decision processes. Mathematical Methods of Operations Research 62, 1, 3–22. DOI: 10.1007/s00186-005-0438-1.

Müller, A. 1997. How does the value function of a markov decision process depend on the transition probabilities? Mathematics of Operations Research 22, 4, 872–885. DOI: 10.1287/moor.22.4.872.

Rachelson, E. and Lagoudakis, M.G. 2010. On the locality of action domination in sequential decision making. Proceedings of 11th international symposium on artificial intelligence and mathematics. Available at: https://oatao.univ-toulouse.fr/17977/.