Typesetting differential equations

Posted on September 18, 2017

This semester I am teaching a course involving linear differential equations, so I have typeset many differential equations that look like this:

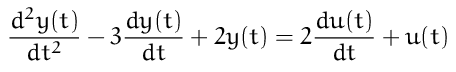
Believe me, writing such equations by hand gets tedious very quickly. So, I wanted a macro \LDE (for Linear Differential Equation), so that I could just type

\LDE{1, -3, 2}{2, 1}

and get the above result. This post describes how to write such a macro using LuaTeX + ConTeXt.

I’ll explain the implementation using a top-down approach. Writing macros in TeX is tough, so let’s delegate all the high lifting to Lua. So, we define a ConTeXt command that simply invokes a Lua function with the appropriate arguments. This can be done using:

\startluacode
-- ... lua function LDE to be added ...
interfaces.definecommand {
    name      = "LDE",
    macro     = LDE,
    arguments = {
        {"content", "list" },
        {"content", "list" },
    }
}
\stopluacode

The name argument specifies the name of the TeX command (\LDE in this case); the macro argument specifies the name of the Lua function (LDE in this case) which gets called when the TeX macro is invoked; the arguments tables specifies the list of arguments of the TeX macros. We specify that the macro has two arguments, both of them are content arguemnts (that is, the macro is invoked as \LDE{...}{...}) and each arguement should be passed on to the Lua function as a list (i.e., a Lua table of strings; other options include hash (for key-value list), number, and string).

Now all we need to do is define the function LDE, which takes two comma separated lists as arguments and typesets the resulting differential equation. The basic logic is straight forward. Suppose we have defined a function derivative that typesets a derivative (taking care of adding a + sign if the coefficient of an intermediate term is positive; not showing the coefficient if the coefficient is +1 or -1; and not showing the term if the coefficient is 0). Then, the LDE function is:

\startluacode
-- Lua function derivative to be added

local LDE = function(LHS, RHS)
  for i = 1, #LHS do
    context(derivative(LHS[i], "y(t)", #LHS - i, i == 1))
  end

  context("=")
  for i = 1, #RHS do
    context(derivative(RHS[i], "u(t)", #RHS - i, i == 1))
  end
end

interfaces.definecommand { ... }
\stopluacode

The last term in the call to the derivative function passes a flag that indicates whether or not the term is the first term.

I’ll not go into the details of the derivative function because it is straight forward. So, here is the complete macro with a usage example:

\startluacode
  local find, format = string.find, string.format

  local derivative = function(coefficient, var, order, first)
    -- If the coefficient is zero or empty, don't typeset anything
    if coefficient == nil or coefficient == "" or coefficient == "0" then
       return
    end

    -- If the coefficient is 1 or -1, we do not want to print the 1.
    if coefficient == "1" then
        coefficient = ""
    elseif coefficient == "-1" then
        coefficient = "-"
    end

    -- If this is not the first coefficient by is a positive coefficient, 
    -- then add a "+" sign
    if not first then
      if find(coefficient, "-") ~= 1 then
         coefficient = "+" .. coefficient
      end
    end

    -- Format the return value depending on the order of the derivative
    local str
    if order == 0 then
       str = format("%s %s", coefficient, var)
    elseif order == 1 then
       str = format("%s \\dfrac{ d %s } { dt }", coefficient, var)
    else
       str = format("%s \\dfrac{ d^{%s} %s } { dt^{%s} }", coefficient, order, var, order)
    end
    return str
  end

  local LDE = function(LHS, RHS)
    LHS = settings_to_array(LHS)
    RHS = settings_to_array(RHS)

    for i = 1, #LHS do
      context(derivative(LHS[i], "y(t)", #LHS - i, i == 1))
    end
    context("=")
    for i = 1, #RHS do
      context(derivative(RHS[i], "u(t)", #RHS - i, i == 1))
    end
  end


interfaces.definecommand {
    name      = "LDE",
    macro     = LDE,
    arguments = {
        {"content", "list" },
        {"content", "list" },
    }
}

\stopluacode

\starttext
\startformula
  \LDE{2,1,-3}{4,0,6}
\stopformula
\startformula
  \LDE{a_2, -a_1,a_0}{b_1,b_0}
\stopformula
\stoptext

---

 <Frame with solid left line | Comibined characters in Math>

This entry was posted in Macros and tagged luatex, programming, separating content and presentation.